*: Petőfi Sándor: Az Alföld című verséből ferdítve,
Mit nekem te zordon Kárpátoknak
Fenyvesekkel vadregényes tája!
Tán csodállak, ámde nem szeretlek,
S képzetem hegyvölgyedet nem járja.
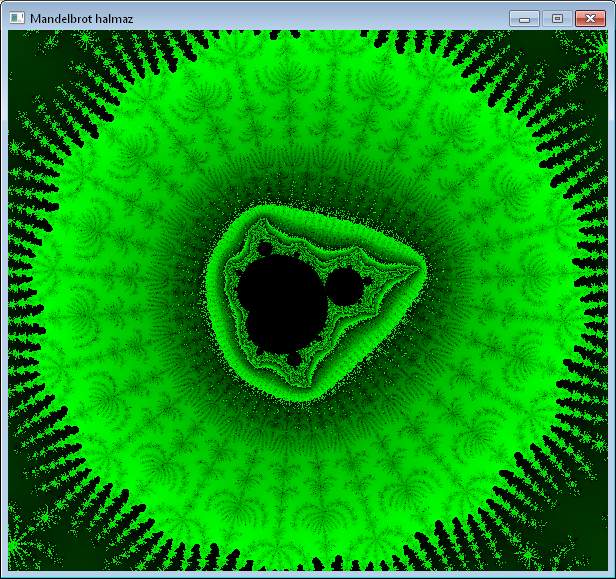
Fogalmam nincs mik a fraktálok. Ködösíteni persze tudok: kompakt halmazok, azaz minden nyílt lefedésükből kiválasztható véges nyílt lefedés (vagy R^n-ben a Heine-Borel tétel következményeként korlátosak és zártak, speciálisan a mutatott kép kapcsán: egy komplex iterációs algoritmus... ) de olyan szinten, mint ahogyan Cantor óta a végtelen fogalmát, vagy Kolmogorov/Chaitin óta a véletlen fogalmát nem értem...
Első "Mandelbrotomat" talán még qbasic-ben (DOS alatt) írtam, a mostani a Páternoszter bevezető C++ példája lesz, egy Qt megvalósítás.
Qt-s állatorvosi ló példánk (ami egyben a "Helló, Világ!"-os példa utáni második bevezető C++ példánk) lesz ez, ezekből a forrásokból indulunk majd ki és finomítunk toövább. A Nokia Qt SDK-t használva ezeket a példákat ugyanúgy élvezheted GNU/Linux és Windows rendszereken is.
A felélesztéshez a Qt Creator-ban készíts egy új Qt Gui App projektet (kattingatás közben a Generate form-ot ne pipáld be, a class neve legyen FrakAblak, aztán majd bal oldalon fent az Edit ikon, hogy lásd a forrásokat, amik közés másold be ezeket, ami van, azt pedig írd fölül.)
Parancssorból így építheted, futtathatod:
[norbi@sgu Frak]$ ls -l main.cpp
összesen 28
-rw-rw-r--. 1 norbi norbi 2917 febr 27 13.46 frakablak.cpp
-rw-rw-r--. 1 norbi norbi 626 febr 27 13.53 frakablak.h
-rw-rw-r--. 1 norbi norbi 4750 febr 27 13.46 frakszal.cpp
-rw-rw-r--. 1 norbi norbi 799 febr 27 13.54 frakszal.h
-rw-rw-r--. 1 norbi norbi 1408 febr 27 13.46 main.cpp
[norbi@sgu Frak]$ qmake-qt4 -project
[norbi@sgu Frak]$ qmake-qt4 Frak.pro
[norbi@sgu Frak]$ make
[norbi@sgu Frak]$./Frak
// main.cpp // // Mandelbrot halmaz rajzoló // Programozó Páternoszter // // Copyright (C) 2011, Bátfai Norbert, nbatfai@inf.unideb.hu, nbatfai@gmail.com // // This program is free software: you can redistribute it and/or modify // it under the terms of the GNU General Public License as published by // the Free Software Foundation, either version 3 of the License, or // (at your option) any later version. // // Bár a Nokia Qt SDK éppen tartalmaz egy Mandelbrotos példát, de // ezt nem tartottam megfelelõnek elsõ Qt programként ajánlani, mert elég // bonyolult: használ kölcsönös kizárást stb. Ezért "from scratch" megírtam // egy sajátot a Javát tanítokhoz írt dallamára: // http://www.tankonyvtar.hu/informatika/javat-tanitok-2-2-080904-1 // #include <QtGui/QApplication> #include "frakablak.h" int main(int argc, char *argv[]) { QApplication a(argc, argv); // További adatokat olvashatsz le innen: // http://www.tankonyvtar.hu/informatika/javat-tanitok-2-3-080904 FrakAblak w1, w2(-.08292191725019529, -.082921917244591272, -.9662079988595939, -.9662079988551173, 600, 3000), w3(-.08292191724880625, -.0829219172470933, -.9662079988581493, -.9662079988563615, 600, 4000), w4(.14388310361318304, .14388310362702217, .6523089200729396, .6523089200854384, 600, 38655); w1.show(); w2.show(); w3.show(); w4.show(); return a.exec(); }
Tekerj a tovább linkre, ha érdekel.
frakablak.h
#ifndef FRAKABLAK_H #define FRAKABLAK_H #include <QtGui/QMainWindow> #include <QImage> #include <QPainter> #include "frakszal.h" class FrakSzal; class FrakAblak : public QMainWindow { Q_OBJECT public: FrakAblak(double a = -2.0, double b = .7, double c = -1.35, double d = 1.35, int szelesseg = 600, int iteraciosHatar = 255, QWidget *parent = 0); ~FrakAblak(); void vissza(int magassag , int * sor, int meret) ; protected: void paintEvent(QPaintEvent*); private: QImage* fraktal; FrakSzal* mandelbrot; }; #endif // FRAKABLAK_H
frakszal.h
#ifndef FRAKSZAL_H #define FRAKSZAL_H #include <QThread> #include <QImage> #include "frakablak.h" class FrakAblak; class FrakSzal : public QThread { Q_OBJECT public: FrakSzal(double a, double b, double c, double d, int szelesseg, int magassag, int iteraciosHatar, FrakAblak *frakAblak); ~FrakSzal(); void run(); protected: // A komplex sík vizsgált tartománya [a,b]x[c,d]. double a, b, c, d; // A komplex sík vizsgált tartományára feszített // háló szélessége és magassága. int szelesseg, magassag; // Max. hány lépésig vizsgáljuk a z_{n+1} = z_n * z_n + c iterációt? // (tk. most a nagyítási pontosság) int iteraciosHatar; FrakAblak* frakAblak; int* egySor; }; #endif // FRAKSZAL_H
frakablak.cpp
// frakablak.cpp // // Mandelbrot halmaz rajzoló // Programozó Páternoszter // // Copyright (C) 2011, Bátfai Norbert, nbatfai@inf.unideb.hu, nbatfai@gmail.com // // This program is free software: you can redistribute it and/or modify // it under the terms of the GNU General Public License as published by // the Free Software Foundation, either version 3 of the License, or // (at your option) any later version. // // This program is distributed in the hope that it will be useful, // but WITHOUT ANY WARRANTY; without even the implied warranty of // MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the // GNU General Public License for more details. // // You should have received a copy of the GNU General Public License // along with this program. If not, see <http://www.gnu.org/licenses/>. // // Ez a program szabad szoftver; terjeszthetõ illetve módosítható a // Free Software Foundation által kiadott GNU General Public License // dokumentumában leírtak; akár a licenc 3-as, akár (tetszõleges) késõbbi // változata szerint. // // Ez a program abban a reményben kerül közreadásra, hogy hasznos lesz, // de minden egyéb GARANCIA NÉLKÜL, az ELADHATÓSÁGRA vagy VALAMELY CÉLRA // VALÓ ALKALMAZHATÓSÁGRA való származtatott garanciát is beleértve. // További részleteket a GNU General Public License tartalmaz. // // A felhasználónak a programmal együtt meg kell kapnia a GNU General // Public License egy példányát; ha mégsem kapta meg, akkor // tekintse meg a <http://www.gnu.org/licenses/> oldalon. // // // Version history: // // 0.0.1 Bár a Nokia Qt SDK éppen tartalmaz egy Mandelbrotos példát, de // ezt nem tartottam megfelelõnek elsõ Qt programként ajánlani, mert elég // bonyolult: használ kölcsönös kizárást stb. Ezért "from scratch" megírtam // egy sajátot a Javát tanítokhoz írt dallamára: // http://www.tankonyvtar.hu/informatika/javat-tanitok-2-2-080904-1 // #include "frakablak.h" FrakAblak::FrakAblak(double a, double b, double c, double d, int szelesseg, int iteraciosHatar, QWidget *parent) : QMainWindow(parent) { setWindowTitle("Mandelbrot halmaz"); int magassag = (int)(szelesseg * ((d-c)/(b-a))); setFixedSize(QSize(szelesseg, magassag)); fraktal= new QImage(szelesseg, magassag, QImage::Format_RGB32); mandelbrot = new FrakSzal(a, b, c, d, szelesseg, magassag, iteraciosHatar, this); mandelbrot->start(); } FrakAblak::~FrakAblak() { delete fraktal; delete mandelbrot; } void FrakAblak::paintEvent(QPaintEvent*) { QPainter qpainter(this); qpainter.drawImage(0, 0, *fraktal); qpainter.end(); } void FrakAblak::vissza(int magassag, int *sor, int meret) { for(int i=0; i<meret; ++i) { QRgb szin = qRgb(0, 255-sor[i], 0); fraktal->setPixel(i, magassag, szin); } update(); }
frakszal.cpp
// frakszal.cpp // // Mandelbrot halmaz rajzoló // Programozó Páternoszter // // Copyright (C) 2011, Bátfai Norbert, nbatfai@inf.unideb.hu, nbatfai@gmail.com // // This program is free software: you can redistribute it and/or modify // it under the terms of the GNU General Public License as published by // the Free Software Foundation, either version 3 of the License, or // (at your option) any later version. // // This program is distributed in the hope that it will be useful, // but WITHOUT ANY WARRANTY; without even the implied warranty of // MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the // GNU General Public License for more details. // // You should have received a copy of the GNU General Public License // along with this program. If not, see <http://www.gnu.org/licenses/>. // // Ez a program szabad szoftver; terjeszthetõ illetve módosítható a // Free Software Foundation által kiadott GNU General Public License // dokumentumában leírtak; akár a licenc 3-as, akár (tetszõleges) késõbbi // változata szerint. // // Ez a program abban a reményben kerül közreadásra, hogy hasznos lesz, // de minden egyéb GARANCIA NÉLKÜL, az ELADHATÓSÁGRA vagy VALAMELY CÉLRA // VALÓ ALKALMAZHATÓSÁGRA való származtatott garanciát is beleértve. // További részleteket a GNU General Public License tartalmaz. // // A felhasználónak a programmal együtt meg kell kapnia a GNU General // Public License egy példányát; ha mégsem kapta meg, akkor // tekintse meg a <http://www.gnu.org/licenses/> oldalon. // // // Version history: // // 0.0.1 Bár a Nokia Qt SDK éppen tartalmaz egy Mandelbrotos példát, de // ezt nem tartottam megfelelõnek elsõ Qt programként ajánlani, mert elég // bonyolult: használ kölcsönös kizárást stb. Ezért "from scratch" megírtam // egy sajátot a Javát tanítokhoz írt dallamára: // http://www.tankonyvtar.hu/informatika/javat-tanitok-2-2-080904-1 // #include "frakszal.h" FrakSzal::FrakSzal(double a, double b, double c, double d, int szelesseg, int magassag, int iteraciosHatar, FrakAblak *frakAblak) { this->a = a; this->b = b; this->c = c; this->d = d; this->szelesseg = szelesseg; this->iteraciosHatar = iteraciosHatar; this->frakAblak = frakAblak; this->magassag = magassag; egySor = new int[szelesseg]; } FrakSzal::~FrakSzal() { delete[] egySor; } // A szál kódját a Javát tanítokhoz írt Java kódomból vettem át // http://www.tankonyvtar.hu/informatika/javat-tanitok-2-2-080904-1 // mivel itt az algoritmust is leírtam/lerajzoltam, így meghagytam // a kommenteket, hogy a hallgató könnyen hozzáolvashassa az "elméletet", // ha érdekli. void FrakSzal::run() { // A [a,b]x[c,d] tartományon milyen sûrû a // megadott szélesség, magasság háló: double dx = (b-a)/szelesseg; double dy = (d-c)/magassag; double reC, imC, reZ, imZ, ujreZ, ujimZ; // Hány iterációt csináltunk? int iteracio = 0; // Végigzongorázzuk a szélesség x magasság hálót: for(int j=0; j<magassag; ++j) { //sor = j; for(int k=0; k<szelesseg; ++k) { // c = (reC, imC) a háló rácspontjainak // megfelelõ komplex szám reC = a+k*dx; imC = d-j*dy; // z_0 = 0 = (reZ, imZ) reZ = 0; imZ = 0; iteracio = 0; // z_{n+1} = z_n * z_n + c iterációk // számítása, amíg |z_n| < 2 vagy még // nem értük el a 255 iterációt, ha // viszont elértük, akkor úgy vesszük, // hogy a kiinduláci c komplex számra // az iteráció konvergens, azaz a c a // Mandelbrot halmaz eleme while(reZ*reZ + imZ*imZ < 4 && iteracio < iteraciosHatar) { // z_{n+1} = z_n * z_n + c ujreZ = reZ*reZ - imZ*imZ + reC; ujimZ = 2*reZ*imZ + imC; reZ = ujreZ; imZ = ujimZ; ++iteracio; } // ha a < 4 feltétel nem teljesült és a // iteráció < iterációsHatár sérülésével lépett ki, azaz // feltesszük a c-rõl, hogy itt a z_{n+1} = z_n * z_n + c // sorozat konvergens, azaz iteráció = iterációsHatár // ekkor az iteráció %= 256 egyenlõ 255, mert az esetleges // nagyítasok során az iteráció = valahány * 256 + 255 iteracio %= 256; //a színezést viszont már majd a FrakAblak osztályban lesz egySor[k] = iteracio; } // Ábrázolásra átadjuk a kiszámolt sort a FrakAblak-nak. frakAblak->vissza(j, egySor, szelesseg); } }
Frak.pro
[norbi@sgu Frak]$ more Frak.pro
######################################################################
# Automatically generated by qmake (2.01a) V febr. 27 13:58:48 2011
######################################################################
TEMPLATE = app
TARGET =
DEPENDPATH += .
INCLUDEPATH += .
# Input
HEADERS += frakablak.h frakszal.h
SOURCES += frakablak.cpp frakszal.cpp main.cpp